1. 문제
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
2. 풀이
Dynamic Programming의 대표적인 문제이다.
원래라면 모든 부분집합을 다 확인해야 하기에 O(2**N)의 시간 복자도를 가지지만, DP를 활용함으로써 시간복잡도를 O(NM)으로 개선시켰다. 다만 여기서 M은 N에 대해 독립적인 값이기 때문에, M이 매우 커진다면 시간복잡도 또한 매우 커진다.
DP문제의 쟁점은 늘 그렇듯 어떻게 problem을 subproblem으로 분할 것인가이다.
그 아이디어에 따라서 다음 두 가지를 설계하는 것이 DP문제의 핵심 목표이다.
- DP배열의 의미
- DP배열의 계산법
problem을 subproblem으로 나누는 방법을 설명한 동영상이다.
한 번 보면 이해가 잘 안가고, 세번 정도 보면 이해가 가는듯한 착각을 할 수 있게 된다.ㅎㅎ
같은 방식으로 problem을 분할하는 문제가 있는데, 이어서 풀었더니 2차원 DP를 익히는데 아주 많이 도움되었다.
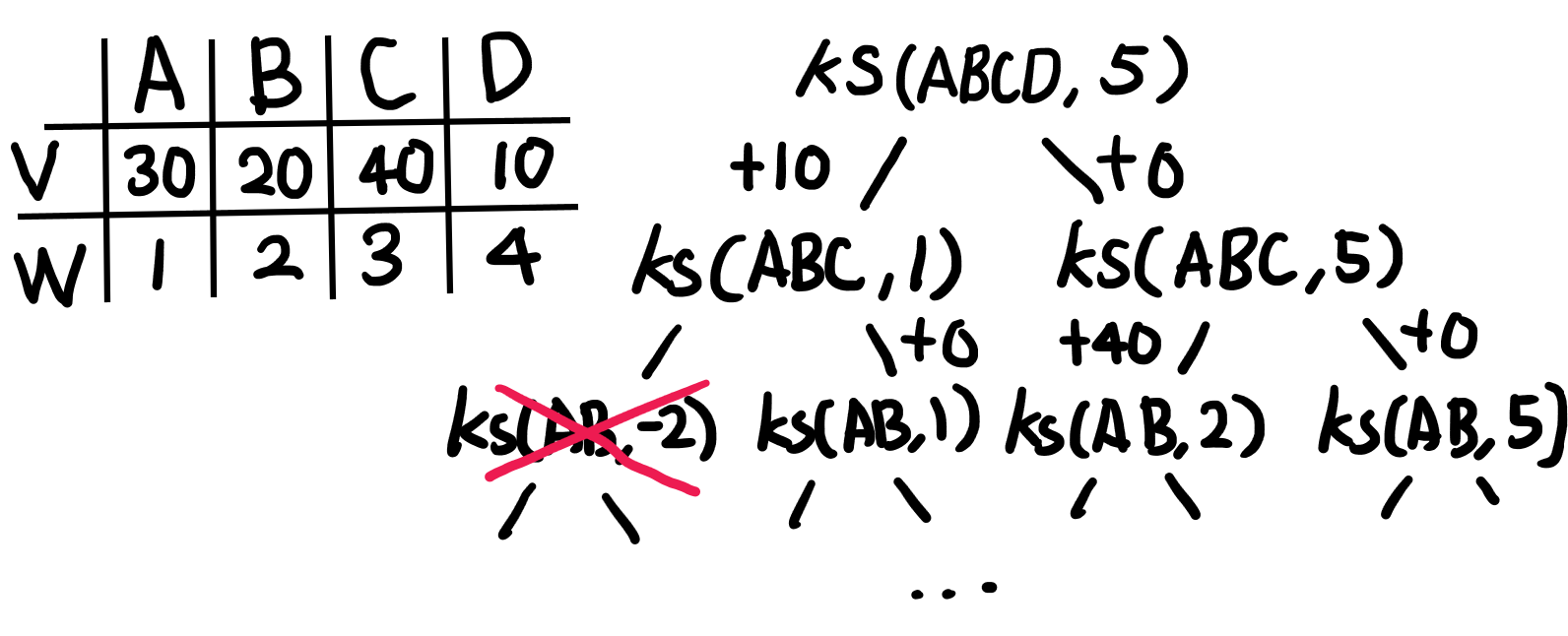
일단 DP배열은 두가지 인자를 가지는 2차원 배열로 설계된다. (물건의 갯수, 가방의 최대 용량)
그리고 DP[n][w] == "1 ~ n까지 n개의 물건이 있고, 가방의 최대용량이 w일 때 담을 수 있는 최대 가치"
[메인 아이디어]
- n > w : n번째 물건이 가방의 최대용량보다 큰 경우
- DP[n][w] = DP[n-1][w] : n번째 물건을 가방에 넣지 못할 수밖에 없다.
n번째 물건을 넣지 않은 경우는, 최대용량이 똑같이 w인 가방에 n-1 개의 물건 중 최대 가치를 고르는 것과 결괏값이 동일하다.
- DP[n][w] = DP[n-1][w] : n번째 물건을 가방에 넣지 못할 수밖에 없다.
- n <= w : n번째 물건이 가방의 최대용량 이하인 경우
- DP[n][w] = max(Case1, Case2) : max(n번째 물건을 넣지 않는 경우, n번째 물건을 넣는 경우)
- Case1 = DP[n-1][w]
가방에 물건의 넣지 않는 경우, 위의 (n>w)과 동일하다. - Case2 = DP[n-1][w - weight_of_n] + value_of_n
n번째 물건을 가방에 넣기 위해서는 적어도 n번째 물건의 무게(weight_of_n)만큼의 빈자리가 있어야 한다. 따라서 최대용량이 (w - weight_of_n) 인 가방에 n-1개의 물건을 최대 가치로 채운 뒤, 거기에 n번째 물건의 가치(value_of_n)를 더한게 n번째 물건을 넣는 경우의 최대 가치다.
- Case1 = DP[n-1][w]
- DP[n][w] = max(Case1, Case2) : max(n번째 물건을 넣지 않는 경우, n번째 물건을 넣는 경우)
DP배열을 결정하는 인자가 2가지 이므로 2차원 배열로 표현된다. 행과 열의 의미는 임의로 정해진 것이기 때문에, 행을 가방의 무게(w)로 열을 물건의 갯수(n)으로 해도 상관은 없다. 그러나 나중에 DP배열을 1차원으로 줄이기 위해서는 지금과 같은 구조가 더 편리하다.
마지막으로 DP배열의 처음값을 설정하는 것도 중요하다. 2차원 배열이므로 0번째 행과 0번째 열을 모두 생각해봐야 한다.
- DP[0][w] : 0개의 물건이 주어졌을 때, 최대용량이 w인 가방에 채울 수 있는 최대 가치 == 0
- DP[n][0] : n개의 물건이 주어졌을 때, 최대용량이 0인 가방에 채울 수 있는 최대 가치 == 0
2.1. 2차원 DP 풀이

가장 기본적인 풀이이다.
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
weight = [0] * (N + 1) # DP배열의 행과 인덱스를 맞추기 위해서 0번째 인덱스 추가
value = [0] * (N + 1) # DP배열의 행과 인덱스를 맞추기 위해서 0번째 인덱스 추가
for i in range(1, N + 1):
weight[i], value[i] = map(int, input().split())
# [1]. 2차원 DP [228MB, 6956ms]
DP = [[0] * (K + 1) for _ in range(N + 1)] # 행: 물건의 갯수 (0 ~ N) / 열: 가방의 최대용량(0 ~ K)
for cur_object in range(1, N + 1): # cur_object: 1부터 N까지 증가
for limit in range(1, K + 1): # limit: 가방의 최대용량을 1부터 K까지 증가
# 메인 아이디어
if weight[cur_object] <= limit: # 현재 물건의 무게가 가방의 최대 용량 이하라면
# 현재 물건을 안 넣는 경우, 현재 물건의 무게만큼 빼고 현재 물건을 넣은 경우 중 큰 것
DP[cur_object][limit] = max(DP[cur_object-1][limit], DP[cur_object-1][limit-weight[cur_object]] + value[cur_object])
else: # 현재 물건의 무게가 가방의 최대 용량 보다 크다면
DP[cur_object][limit] = DP[cur_object - 1][limit] # 현재 물건을 넣지 못한다
print(DP[-1][-1])2.2. 1차원 DP 풀이

1차원 DP라고해서 특별한 것은 아니다. 시간복잡도는 2차원 DP와 동일하다.
다만 DP배열의 n행 계산 시 n-1행의 값만을 참조하는 특징을 이용해 DP배열을 1차원으로 줄여보겠다는 것이다.
(그래서 결과를 보아도 시간은 드라마틱하게 증가하지 않은 반면, 메모리양이 많이 줄어든 것을 확인할 수 있다.)
만일 DP배열의 n행 계산 시 n-1이외의 행을 참조한다면, DP배열을 1차원으로 줄일 수 없다. [백준 2758번 로또] 문제가 그러했다.
단, DP배열을 뒤에서부터 계산해야한다는 것만 주의하면 된다.
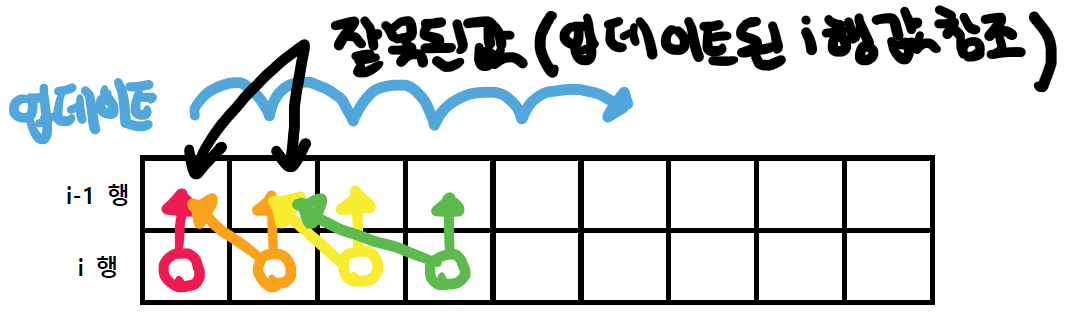
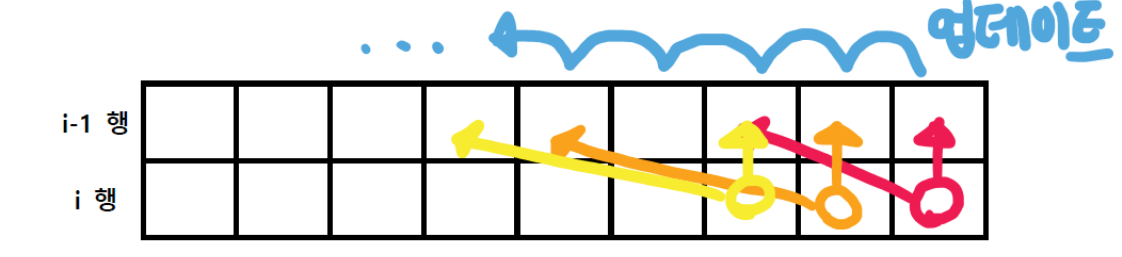
이는 직접 그림을 그려보면 쉽게 확인할 수 있는데, DP[n][w] 값을 계산한다고 할 때, DP[n-1][w]와 DP[n-w][w-weight_of_n]의 값을 참조해야 한다. 즉 DP[n][w]의 상측과 좌상측 값을 참조해야하는데, DP배열 갱신이 왼쪽부터 이루어지면 좌상측 값을 참조할 수 없게 된다. 이미 좌상측 값이 n행의 값으로 엄데이트가 되었기 때문이다.
아래 그림은 설명을 위해서 2개의 행으로 그렸지만, 실제로는 1차원으로 계산된 i행의 특정 열값이 i-1행의 값을 동일 열값을 대체한다.
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
weight = [0] * (N + 1) # DP배열의 행과 인덱스를 맞추기 위해서 0번째 인덱스 추가
value = [0] * (N + 1) # DP배열의 행과 인덱스를 맞추기 위해서 0번째 인덱스 추가
for i in range(1, N + 1):
weight[i], value[i] = map(int, input().split())
# [2]. 1차원 DP [34MB, 5140ms]
DP = [0] * (K + 1)
for cur_object in range(1, N + 1):
for limit in range(K, 0, -1): # 뒤에서 부터 갱신해야지지 DP[cur_object-1][]값을 유효하게 참조할 수 있다.
if limit >= weight[cur_object]: # 현재 물건의 무게가 가방의 최대 용량 이하라면
DP[limit] = max(DP[limit], DP[limit-weight[cur_object]] + value[cur_object]) # 현재 물건을 안 넣는 경우, 현재 물건의 무게만큼 빼고 현재 물건을 넣은 경우 중 큰 것
# 현재 물건의 무게가 가방의 최대 용량 보다 큰 경우, 위의 열의 값을 그대로 가져오는데
# 이미 1차원 DP배열에는 해당값을 가지고 있으므로 따로 처리해 줄 필요가 없다.
print(DP[-1])2.3. 메모이제이션 풀이
많은 경우, DP와 memoization은 서로 상호변환될 수 있다.
DP가 반복문을 이용한 Bottom-Up 방식이었다면, memoization은 재귀호출을 통한 Top-Down 방식으로 구현된다.
보통 재귀호출 한다하면 반복문에 비해 시간이 오래 걸린다고 생각할 수 있다.
하지만 아래 그림에서 볼 수있는 것처럼, 이 문제의 경우 Top-Down방식으로 구현하면 배열의 모든값을 구현할 필요가 없다. 실제로 코드를 실행시켰을 때 가장 짧은 처리시간을 보였다.
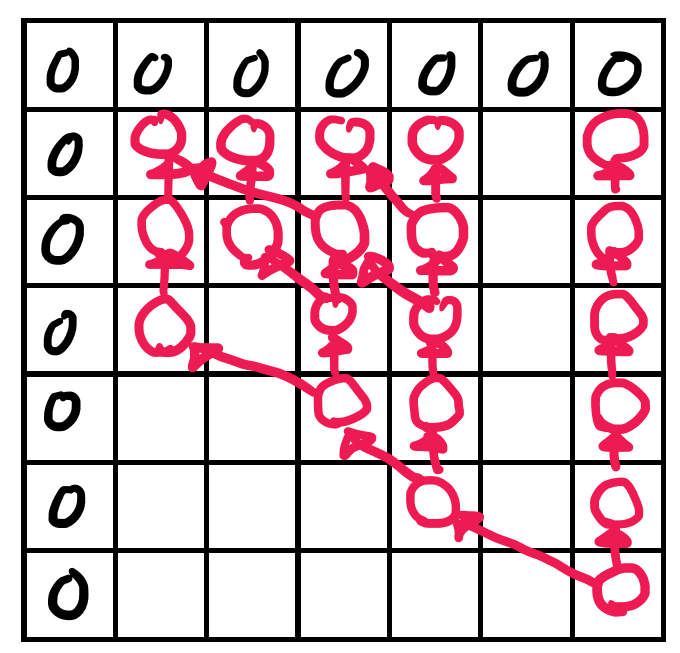
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
weight = [0] * (N + 1) # DP배열의 행과 인덱스를 맞추기 위해서 0번째 인덱스 추가
value = [0] * (N + 1) # DP배열의 행과 인덱스를 맞추기 위해서 0번째 인덱스 추가
for i in range(1, N + 1):
weight[i], value[i] = map(int, input().split())
# [3]. 메모이제이션 [139MB, 3048ms]
def memoization(i, j):
if i <= 0 or j <= 0: # 베이스 반환 조건
return 0
if DP[i][j]: # 저장된 DP값이 있으면, 해당 값을 반환
return DP[i][j]
# 메인 아이디어 코드
if j >= weight[i]: # n번째 물건의 무게가 배낭의 최대 무게 이하면
DP[i][j] = max(memoization(i-1, j), memoization(i-1, j-weight[i]) + value[i]) # 물건을 배낭에 넣지 않거나, 물건 무게 만큼 비우고 물건을 넣는 경우 중 가치가 큰것을 선택한다.ㄹ
else: # n번째 물건의 무게가 배낭의 최대 무게보다 크면
DP[i][j] = memoization(i-1, j) # 물건을 배낭에 넣지 않는다.
return DP[i][j]2.4. 메모이제이션 없는 재귀호출 풀이

그냥 메모이제이션 없이, 즉 연산결과를 저장하지 않으면 얼마나 걸리까 싶어서 코드를 돌려보았다.
좀 더 걸리겠거니 했는데 아예 시간초과가 나버렸다.
import sys
input = sys.stdin.readline
N, K = map(int, input().split())
weight = [0] * (N + 1) # DP배열의 행과 인덱스를 맞추기 위해서 0번째 인덱스 추가
value = [0] * (N + 1) # DP배열의 행과 인덱스를 맞추기 위해서 0번째 인덱스 추가
for i in range(1, N + 1):
weight[i], value[i] = map(int, input().split())
# [4]. 메모이제이션 없는 재귀호출 [시간초과]
def recursive(i, j):
if i <= 0 or j <= 0:
return 0
if j >= weight[i]:
return max(recursive(i-1, j), recursive(i-1, j-weight[i]) + value[i])
else:
return recursive(i-1, j)
print(recursive(N, K))'Code Review > BaekJoon' 카테고리의 다른 글
| [ 백준 1922번 네트워크 연결 ] Python 코드 (MST) (0) | 2022.10.26 |
|---|---|
| [ 백준 21610번 마법사 상어와 비바라기 ] Python 코드 (Simulation) (0) | 2022.10.24 |
| [ 백준 2156번 포도주 시식 ] Python 코드 (DP) (0) | 2022.10.24 |
| [ 백준 9465번 스티커 ] Python 코드 (DP) (0) | 2022.10.24 |
| [ 백준 1890번 점프 ] Python 코드 (DP) (1) | 2022.10.14 |



